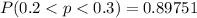Answer:
The probability is
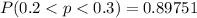
Explanation:
From the question we are told that
The population proportion is p = 0.25
The sample size is n = 200
Generally given that the sample size is large the mean of this sampling distribution is mathematically represented as
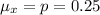
Generally the standard deviation is mathematically represented as
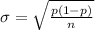
=>
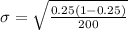
=>
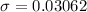
Generally the probability that between 20% (0.2) to 30% (0.3) of the households in the sample have a burglar alarm is mathematically represented as
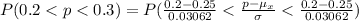
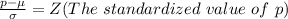
=>
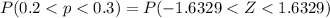
=>
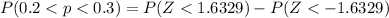
From the z table the area under the normal curve to the left corresponding to 1.6329 and -1.6329 is
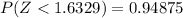
and
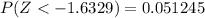
So
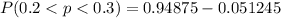
=>