Question

An apartment complex allows residents to have up to 3 dogs and up to 2 cats. The joint probability model for the number of dogs (X) and number of cats (Y) that a resident has, is given below. Given that a resident has 1 cat, what is the probability that the resident does not have any dog

Answer 1

Complete Question

The complete question is shown on the first uploaded image

Answer:

The correct option is the second option

Explanation:

Let D be the event that a resident has a dog

Let C be the event that a resident has a cat

Generally according to Bayes rule the probability that a resident has no dog give that he/she has one cat is mathematically represented as

`P(D' | C) = (P ( D' \ n \ C))/( P( C ))`

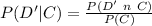
Here
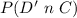`P(D' \ n \ C )` is the probability that a resident has one cat and no dog and from the table the value is

`P(D' \ n \ C ) = 0.2`

and
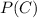`P(C)` is the probability of having one cat which is mathematically evaluated as

`P(C) = P(C \ n \ D') + P(C \ n \ D) + P(C \ n \ 2D) + P(C \ n \ 3D)`

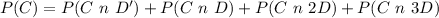
From the table

P(C \ n \ D') = 0.2

P(C \ n \ D) = 0.05

P(C \ n \ 2D) = 0.04

P(C \ n \ 3D) = 0.06

`P(C) = 0.2 + 0.05 + 0.04 + 0.06`

=>
`P(C) = 0.35`

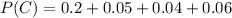
So

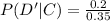
`P(D' | C) = (0.2)/( 0.35)`

=>
`P(D' | C) = (4)/(7)`