Complete Question
Although the first quarter of 2002 was quite dismal on Wall Street, mutual funds investing in gold companies rose an average of 35.2%. Assume that the distribution of returns in the first quarter of 2002 for mutual funds specializing in gold companies is fairly symmetrical with a mean of 35.2% and a standard deviation of 20%. If random samples of 16 gold stock funds were selected:
90% of the sample mean returns are between what two values symmetrically distributed around the mean?
Answer:
The two values symmetrically distributed around the mean are
21.87\% and 43.17\%
Explanation:
From the question we are told that
The sample size is

The sample mean is
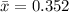
The standard deviation is
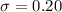
Generally the degree of freedom is mathematically represented as

=>

=>
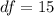
From the question we are told the confidence level is 90% , hence the level of significance is
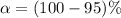
=>
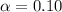
Generally from the t distribution table the critical value of
 at a degree of freedom of
at a degree of freedom of
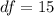 is
is
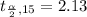
Generally the margin of error is mathematically represented as
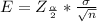
=>
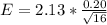
=>
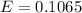
Generally 90% confidence interval is mathematically represented as
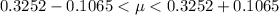
=>

converting to percentage
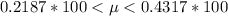
=>
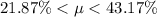
Hence the 90% of the sample mean returns are between 21.87\% and 43.17\%