Answer:
The rate of change in the area beneath the ladder is 5.25 ft²/s
Explanation:
Area of triangle is given by;
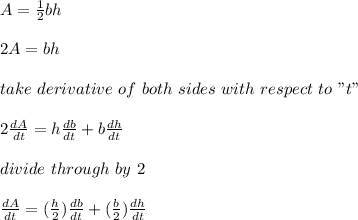
where;
b is the base of the triangle, given as 6 ft
h is the height of the triangle, determined by applying Pythagoras theorem.
h² = 10² - 6²
h² = 100 - 36
h² = 64
h = √64
h = 8 ft
Determine the rate of change of the height;
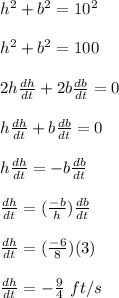
Finally, determine the rate of change of area beneath the ladder;
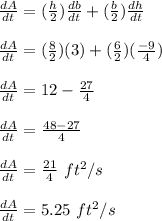
Therefore, the rate of change in the area beneath the ladder is 5.25 ft²/s