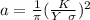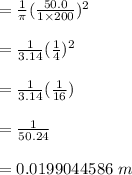Answer:
The answer is "
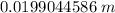 ".
".
Step-by-step explanation:
The crucial stress essential for activating the spreading of the crack is
 , the hardness of the strain break is K, as well as the area long of a break is a, for dimensionless Y. Its equation of the length of its surface of the fracture is 50.1 MPa
, the hardness of the strain break is K, as well as the area long of a break is a, for dimensionless Y. Its equation of the length of its surface of the fracture is 50.1 MPa
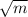 on K, 200MPa on
on K, 200MPa on
 , and 1 on Y.
, and 1 on Y.