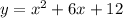1 Answer

Rftr · Answer 1 · 2023-09-15T12:00:33+0000

Answer:

Calculate the first differences between the y-values:

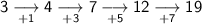
$\sf 3 \underset{+1}{\longrightarrow} 4 \underset{+3}{\longrightarrow} 7 \underset{+5}{\longrightarrow} 12 \underset{+7}{\longrightarrow} 19$

As the first differences are not the same, we need to calculate the second differences:

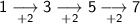
$\sf 1 \underset{+2}{\longrightarrow} 3 \underset{+2}{\longrightarrow} 5 \underset{+2}{\longrightarrow} 7$

As the second differences are the same, the relationship between the variable is quadratic and will contain an
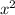x^2 term.

--------------------------------------------------------------------------------------------------

To determine the quadratic equation

The coefficient of
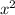x^2 is always half of the second difference.

As the second difference is 2, and half of 2 is 1, the coefficient of
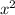x^2 is 1.

The standard form of a quadratic equation is:
y=ax^2+bx+c

(where a, b and c are constants to be found).

We have already determined that the coefficient of
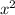x^2 is 1.

Therefore, a = 1

From the given table, when
x=0 ,
y=12 .

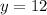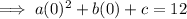
$\implies a(0)^2+b(0)+c=12$

$\implies c=12$

Finally, to find b, substitute the found values of a and c into the equation, then substitute one of the ordered pairs from the given table:

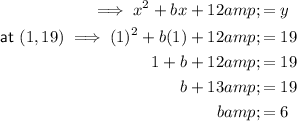
$\begin{aligned}\implies x^2+bx+12 & = y\\ \textsf{at }(1,19) \implies (1)^2+b(1)+12 & = 19\\ 1+b+12 & = 19\\b+13 & =19\\b&=6\end{aligned}$

Therefore, the quadratic equation for the given ordered pairs is:

y=x^2+6x+12

Please log in or register to add a comment.