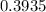Answer:
The probability is
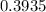
Explanation:
We know that the time it takes a worker on an assembly line to complete a task is exponentially distributed with a mean of 8 minutes.
Let's define the random variable ⇒
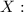 '' The time it takes a worker on an assembly line to complete a task ''
'' The time it takes a worker on an assembly line to complete a task ''
We know that
 is exponentially distributed with a mean of 8 minutes ⇒
is exponentially distributed with a mean of 8 minutes ⇒
 ~ Exp (λ)
~ Exp (λ)
Where '' λ '' is the parameter of the distribution.
Now, the mean of an exponential distribution is ⇒
 1 / λ (I)
1 / λ (I)
We have the value of the mean ''
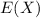 '' , then we replace that value in the equation (I) to obtain the parameter λ ⇒
'' , then we replace that value in the equation (I) to obtain the parameter λ ⇒
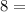 1 / λ ⇒
1 / λ ⇒
λ =

Then ,
 ~
~

The cumulative distribution function of
 is :
is :
 when
when
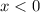 and
and
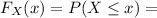 1 - e ^ ( - λx) when
1 - e ^ ( - λx) when
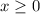 (II)
(II)
If we replace the value of the parameter in (II) :
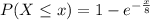 when
when
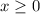
We need to calculate
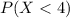
Given that
 is a continuous random variable :
is a continuous random variable :

We use the cumulative distribution function to calculate the probability :
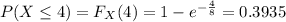
The probability is