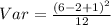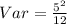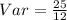Question

Product codes of 2, 3, 4, 5, or 6 letters are equally likely. What is the mean and variance of the number of letters in the codes

Answer 1

`Mean = 4`

`Var = (25)/(12)`

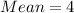
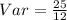
Explanation:

Given

Codes: 2,3,4,5,6

Required

Determine the Mean and Variance

Equally likely implies that the data follows a uniform distribution.

So,

`Mean = (a+b)/(2)`

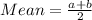
Where

`a = Lower\ Bound = 2`

`b = Upper\ Bound = 6`

`Mean = (a+b)/(2)`

`Mean = (2 + 6)/(2)`

`Mean = (8)/(2)`

`Mean = 4`

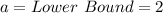
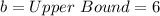
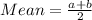
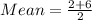
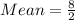
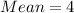
Variance of a uniform distribution is calculated as thus;

`Var = ((b-a+1)^2)/(12)`

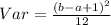
Substitute values for a and b

`Var = ((6-2+1)^2)/(12)`

`Var = (5^2)/(12)`

`Var = (25)/(12)`