Answer:

Step-by-step explanation:
We are asked to find the time it takes for a mango to fall 20 meters.
We know the distance, acceleration, and initial velocity, so we will use the following kinematic equation:
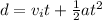
The mango is dropped from rest, so the initial velocity is 0 meters per second. It falls a distance of 20 meters. The acceleration due to gravity is 10 meters per second squared.
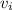 = 0 m/s
= 0 m/s - d= 20 m
- a= 10 m/s²
Substitute the values into the equation.
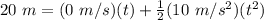
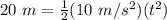
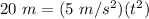
We are solving for time, so we must isolate the variable t. It is being multiplied by 5 meters per second squared. The inverse operation of multiplication is division, so divide both sides by 5 m/s².
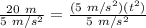
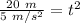
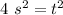
The variable t is being squared. Take the square root of both sides.
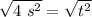
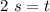
It takes 2 seconds for a mango to fall 20 meters.