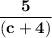Question

Divide Rational Expressions
In the following exercises, divide.

Answer 1

`\displaystyle \mathbf{(5)/((c+4))}`

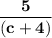
Explanation:

Division of Rational Expressions

When dividing two rational expressions like f(c) / g(c), it's usually easier to multiply the numerator by the reciprocal of the denominator: f(c) * (1/g(c)). The reciprocal is just flipping the numerator and the denominator.

Let's find the following division:

`\displaystyle \frac{(c^2-64)/(3c^2+26c+16)} {(c^2-4c-32)/(15c+10)}`

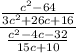
First, we factor the polynomials where possible.

`c^2-64 = (c-8)(c+8)`

`3c^2+26c+16=(3c+2)(c+8)`

`c^2-4c-32=(c-8)(c+4)`

`15c+10=5(3c+2)`

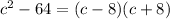
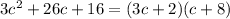
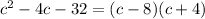
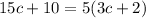
Substituting:

`\displaystyle \frac{(c^2-64)/(3c^2+26c+16)} {(c^2-4c-32)/(15c+10)}=\frac{((c-8)(c+8))/((3c+2)(c+8))} {((c-8)(c+4))/(5(3c+2))}`

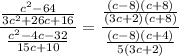
Multiplying by the reciprocal of the denominator:

`\displaystyle \frac{(c^2-64)/(3c^2+26c+16)} {(c^2-4c-32)/(15c+10)}=((c-8)(c+8))/((3c+2)(c+8))\cdot (5(3c+2))/((c-8)(c+4))`

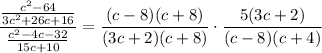
Simplifying by (c+8)(3c+2)(c-8):

`\displaystyle \frac{(c^2-64)/(3c^2+26c+16)} {(c^2-4c-32)/(15c+10)}=(5)/((c+4))`

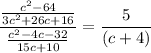
Answer:

`\displaystyle \mathbf{\mathbf{(5)/((c+4))}}`