Question

Find m< x (Type the number answer)

Answer 1

x=74.73°

Explanation:

Law of cosines

In a general triangle, the law of cosines relates the lengths of the sides of the triangle to the cosine of one of its angles.

The law of cosine is expressed as:

`\displaystyle c^(2)=a^(2)+b^(2)-2ab\cos x`

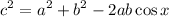
Where a and b are the lengths of two sides of the triangle, x is the angle contained between them, and c is the other side length.

If all side lengths are known, we can solve the above equation for the angle x:

`\displaystyle x =\arccos \left({\frac {a^(2)+b^(2)-c^(2)}{2ab}}\right)`

From the image, we must select a and b as the sides adjacent to angle x in any order. Thus a=17, b=22, c=24. Substituting:

`\displaystyle x=\arccos \left({\frac {17^(2)+22^(2)-24^(2)}{2(17)(22)}}\right)`

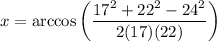
Operating:

`\displaystyle x=\arccos \left({\frac {289+484-576}{748}}\right)`

`\displaystyle x=\arccos \left({\frac {197}{748}}\right)`

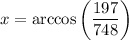
Using a scientific calculator:

x=74.73°