Question

Which description of the vector shown is correct ?

• The magnitude is 7sqrt2, and the direction angle is approximately 315 degrees
• The magnitude is 7sqrt2, and the direction angle is approximately 135 degrees
•The magnitude is sqrt6, and the direction angle is approximately 315 degrees

• The magnitude is sqrt6, and the direction angle is approximately 135 degrees

Answer 1

B

Explanation:

Answer 2

(B) The magnitude is 7sqrt2, and the direction angle is approximately 135 degrees.

Explanation:

From the figure, the coordinate of the tail of the vector,

`(x_1,y_1)=(3,-6).`

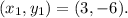
The coordinate of the head of the vector,

`(x_2,y_2)=(-4,1).`

The magnitude of a vector is the length between the head and tail of the vector.

By using the distance formula,

the magnitude of the vector
`= √((1-(-6))^2+(-4-3)^2)`

`=√((7^2+(-7)^2)\\\\=√(98)\\\\=7√(2)`

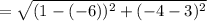
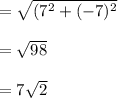
Now, let
`\theta` be the angle made by the vector with the positive direction of the x-axis, so

`\tan\theta = (y_2-y_1)/(x_2-x_1)\\\\\Rightarrow \tan\theta = (1-(-6))/(-4-3)=(7)/(-7)=-1 \\\\\Rightarrow \theta = \tan^(-1)(-1) \\\\\Rightarrow \theta =\pi- \tan^(-1)1 \\\\\Rightarrow \theta = \pi-(\pi)/(4) \\\\\Rightarrow \theta =(3\pi)/(4) \\\\\Rightarrow \theta = 135 ^(\circ).`

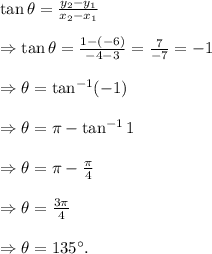
So, the magnitude of the vector is
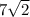`7\sqrt 2` which makes
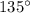`135 ^(\circ)` with the positive direction of the x-axis.

Hence, option (B) is correct.