Question

Help please!!! I messed up on the first question I asked, but this one is right!

Answer 1

1) m=2/3

2) b=10

3) x-int:(-15, 0)

4) y-int: (0, 10)

Our equation is:

`y=(2)/(3)x+10`

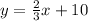
Explanation:

To start, let’s find the equation of the line.

We can use the point-slope form:

`y-y_1=m(x-x_1)`

Where m is the slope and (x₁, y₁) is a point.

So, let’s substitute 2/3 for m and (-3, 8) for (x₁, y₁). This yields:

`y-8=(2)/(3)(x-(-3))`

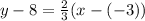
Simplify:

`y-8=(2)/(3)(x+3)`

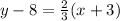
Distribute:

`y-8=(2)/(3)x+2`

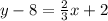
Add 8 to both sides:

`y=(2)/(3)x+10`

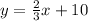
This is in slope intercept form: y=mx+b.

Therefore, our m is 2/3 and our b is 10.

To find the x-intercept, we will substitute 0 for y and solve for x. Therefore:

`0=(2)/(3)x+10`

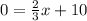
Subtract 10 from both sides:

`-10=(2)/(3)x`

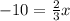
Multiply both sides by 3/2. So:

`x=-10((3)/(2))=-30/2=-15`

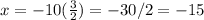
Therefore, the x-intercept is (-15, 0).

To find the y-intercept, we will substitute 0 for x and solve for y. Therefore:

`y=(2)/(3)(0)+10=10`

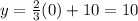
So, the y-intercept is (0, 10).

We will also graph it. See the attachment. To graph by hand, we can start at the y-intercept and go up two for every three to the right. Or, we can go down two for every three to the left. This should yield the following graph: