Answer:
A. The function that gives the height of the bowling ball after t seconds is
![h(t) = 50-16.087\cdot t^(2)\,\,\,[ft]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ee4ft8gm9tc8dt2r3ljb3mwfz8k3c37jib.png) .
.
B. The height of the bowling ball after 1 second is 33.913 feet.
C. The bowling ball will take approximately 1.763 seconds to hit the ground.
Explanation:
A. From Physics we notice that ball experiments a free-fall, which is an uniform accelerated motion due to gravity and where air friction and effects of the Earth's rotation are neglected. The height of the ball is described by the following kinematic equation:
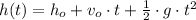 (1)
(1)
Where:
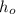 - Initial height of the ball, measured in feet.
- Initial height of the ball, measured in feet.
 - Initial velocity of the ball, measured in feet per second.
- Initial velocity of the ball, measured in feet per second.
 - Time, measured in seconds.
- Time, measured in seconds.
 - Gravitational acceleration, measured in feet per square second.
- Gravitational acceleration, measured in feet per square second.
If we know that
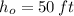 ,
,
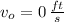 and
and
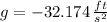 , then the function that gives the height of the bowling ball after t seconds is:
, then the function that gives the height of the bowling ball after t seconds is:
![h(t) = 50-16.087\cdot t^(2)\,\,\,[ft]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ee4ft8gm9tc8dt2r3ljb3mwfz8k3c37jib.png) (2)
(2)
The function that gives the height of the bowling ball after t seconds is
![h(t) = 50-16.087\cdot t^(2)\,\,\,[ft]](https://img.qammunity.org/2021/formulas/mathematics/high-school/ee4ft8gm9tc8dt2r3ljb3mwfz8k3c37jib.png) .
.
B. If we know that
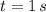 , then the height of the bowling ball is:
, then the height of the bowling ball is:


The height of the bowling ball after 1 second is 33.913 feet.
C. The bowling ball hits the ground when height is zero. Let equalize (1) to zero and solve the resulting expression:

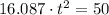

The bowling ball will take approximately 1.763 seconds to hit the ground.