Let
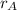 and
and
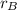 be the respective radii of balloons A and B. If the fixed total volume is V, then
be the respective radii of balloons A and B. If the fixed total volume is V, then
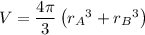
and knowing
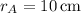 and
and
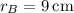 at the start, we have V = 6916π/3 cm³. Then when
at the start, we have V = 6916π/3 cm³. Then when
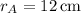 , the radius of the other sphere is
, the radius of the other sphere is
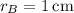 .
.
Differentiating both sides with respect to time t gives a relation between the rates of change of the radii:

We're given
 the whole time. At the moment
the whole time. At the moment
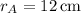 , the radius of balloon B is changing at a rate of
, the radius of balloon B is changing at a rate of
