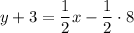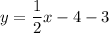Answer:
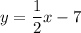
Explanation:
Perpendicular Lines
Two lines of slopes m1 and m2 are perpendicular if their slopes meet the condition:
![m_1\cdot m_2=-1\qquad \qquad [1]](https://img.qammunity.org/2021/formulas/mathematics/high-school/tw5caqyx0p6mvg2tvy7gibmjp0obweve06.png)
The slope-intercept form of a line with slope m and y-intercept of b is:

The point-slope form of a line with slope m that passes through the point (h,k) is:
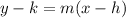
We are given the line
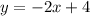
From which we can know the value of the slope is m1=-2
The slope of the required line m2 can be calculated from [1]
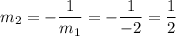
Now we know the slope and the point (8,-3) through which our line goes, thus:
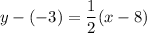
To find the slope-intercept form, operate: