Question

2x^{3}+30xx^{2} +72x=0 solve using zero product property

Answer 1

Values of x are: x=0 or x=-3 or x=-12

Explanation:

The equation given to solve using zero product property is
`2x^3+30x^2+72x=0`

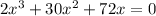
Zero property rule states that if ab=0 then a=0 or b=0

Taking x common from the equation:

`2x^3+30x^2+72x=0\\x(2x^2+30x+72)=0\\`

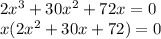
Applying zero product rule

`x(2x^2+30x+72)=0\\x=0 \ or \ 2x^2+30x+72=0`

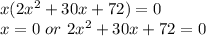
Now, solving
`2x^2+30x+72=0`

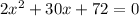
Using quadratic formula to find value of x

`$x=(-b\pm√(b^2-4ac))/(2a)$`

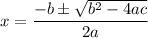
Putting values

`$x=(-30\pm√((30)^2-4(2)(72)))/(2(2))$\\$x=(-30\pm√(324))/(4)$\\$x=(-30\pm18)/(4)$\\$x=(-30+18)/(4) \ or \ x=(-30-18)/(4)$ \\x=-3 \ or \ x=-12`

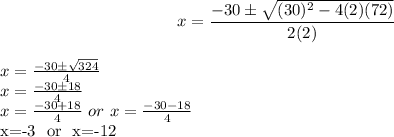
So, Values of x are: x=0 or x=-3 or x=-12