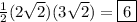Answer:
Explanation:
Note that in this diagram, point A represents point X, point B represents point Y, and point C represents point Z.
From the diagram, it appears as if
 . To determine if this is the case, we can find the slopes of both segments.
. To determine if this is the case, we can find the slopes of both segments.
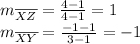
Since these slopes are negative reciprocals, we know that they are perpendicular.
This means we can use the formula
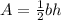 , where b is the base (XY) and h is the height (XZ).
, where b is the base (XY) and h is the height (XZ).
- Note these are interchangeable.
Using the distance formula,
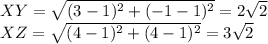
This means the area is