Evaluate: \bf{\sum^6_(n=0\:)(3)^n} Need help A.S.A.P., thank you! :)

Question

Evaluate:


`\bf{\sum^6_(n=0\:)(3)^n}`



Need help A.S.A.P., thank you! :)

Answer 1

`\boxed{\rm \: SUM = 1093 }`

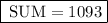
Step-by-step explanation:

Given:

`\huge\rm {{ \sum}^6_(n=0\:) (3)^n}`

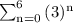
To Find:

Sum of the given finite series

Solution:

We'll use this formula:

`\boxed{\rm SUM = a \cdot\bigg( \cfrac{1 - r {}^(n) }{1 - r} \bigg)}`

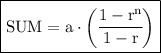
where,

• a = first term
• r = ratio in between terms

Let's find out the ratio R by using this formulae:

`\rm \: r = \cfrac{a_(n + 1) }{a_n}`

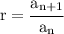
According to the question,

• 
  `\rm a_n = 3^n`
• 
  `\rm a_(n+1)= 3^(n+1)`

Substitute:

`\rm \: r = \cfrac{3 {}^(n + 1) }{3 {}^(n) }`

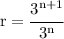
Apply law of exponents:[a^m/a^n] = a^m-n

`\rm \: r = {3}^(n + 1 - n)`

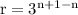
Rearrange it as:

`\rm \: r = 3 {}^(n - n + 1)`

`\rm \: r = 3 {}^(1) = 3`

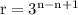
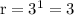
So,the ratio R is 3.

Now let's find out the First term A.

To find, substitute the value of n in 3^n:

• [It is given that n = 0]

`\rm \: a = 3 {}^(0)`

• [x^0 = 1]

`\rm \: a = 1`

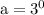
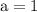
Hence, first term A is 1.

NOW Substitute the value of the first term A and ratio R onto the formulae of sum:

`\rm \: a \cdot\bigg( \cfrac{1 - r {}^(n) }{1 - r} \bigg)`

• a = 1
• r = 3
• n = 7

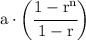
Simplify.

`\rm SUM = \rm \: 1 * \cfrac{1 - 3 {}^(7) }{ 1 - 1 * 3}`

`\rm \: SUM = \cfrac{ - 2186}{1 - 3}`

`\rm \: SUM = \cfrac{ \cancel{ - 2186} \: \: {}^(1093) }{ \cancel{ - 2} \: \: ^(1) }`

`\rm \: SUM = 1093`

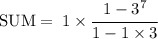
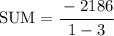
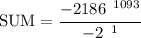
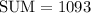
We're done!

Hence, the sum of the given Finite series is 1093.

`\rule{225pt}{2pt}`

Answer 2

1093

Step-by-step explanation:

Given expression:

• 
  `\sf \huge{ \sum _(n=0)^6\left(3\right)^n}`

Summation:

• 
  `\sf a_0+\sum _(n=1)^63^n`

Formula:

• 
  `\sf \sum\limits_(i=1)^n x_i = x_1 + x_2 + \dots + x_n`

Compute:

`\rightarrow \sf 3^0 + 3^1 + 3^2 + 3^3 + 3^4 + 3^5 + 3^6`

`\rightarrow \sf 1 + 3 + 9 + 27 + 81 + 243 + 729`

`\rightarrow \sf 1093`