Question

What is the slope of the line that contains the points (-2, 2) and (3, 4)?

A.
O B. -
O c.
OD.

Answer 1

Answer: m = 2/5

Explanation:

The formula for the slope is m = rise over run = y^2 - y^1 / x^2 - x^2

which makes it 4-2 over 3-(-2) which equals 2/5

Youre answer is 2/5

Answer 2

The slope of the line that contains the points (-2, 2) and (3, 4) is 2/5.

Explanation:

The slope of a line is denoted by m and is calculated using the formula:

`m = (y_2-y_1)/(x_2-x_1)`

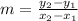
Here

`(x_1,y_1)` are the coordinates of the first point on line and

`(x_2,y_2)` are the coordinates of the second point on line

Given two points are:

(x1,y1) = (-2, 2)

(x2,y2) =(3, 4)

Putting the values in the formula

`m = (4-2)/(3-(-2))\\m = (2)/(3+2)\\m=(2)/(5)`

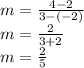
Hence,

The slope of the line that contains the points (-2, 2) and (3, 4) is 2/5.