Question

A brand new car costs $18,000, this price depreciates at 25% every year, how much would the car be after 12 years? 20 years?

Answer 1

C(12)=$570.18

C(20)=$57.08

Explanation:

Exponential Decay Function

The exponential function is often used to model natural growing or decaying processes, where the change is proportional to the actual quantity.

An exponential decaying function is expressed as:

`C(t)=C_o\cdot(1-r)^t`

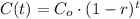
Where:

C(t) is the actual value of the function at time t

Co is the initial value of C at t=0

r is the decaying rate, expressed in decimal

The depreciation of goods is often modeled as an exponential function. The new car costs $18,000 and its price depreciates at r=25%= 0.25 every year.

The depreciation model is:

`C(t)=18,000\cdot(1-0.25)^t`

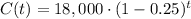
Operating:

`C(t)=18,000\cdot 0.75^t`

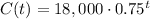
At t=12 years, the price will be:

`C(12)=18,000\cdot 0.75^(12)`

C(12)=$570.18

At t=20 years, the price will be:

`C(20)=18,000\cdot 0.75^(20)`

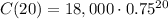
C(20)=$57.08