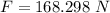Question

A golf ball (m=26.7g) is struck a blow that makes an angle of 33.6 degrees with the horizontal. The drive lands 190m away on a flat fairway. The acceleration of gravity is 9.8 m/s^2 . If the golf club and ball are in contact for 7.13 ms, what is the average force of impact?

Answer 1

Th average force impact is
`F = 168.298 \ N`

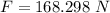
Step-by-step explanation:

From the question we are told that

The mass of the golf ball is
`m_g = 26.7 \ g = 0.0267 \ kg`

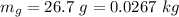
The angle made is
`\theta = 33.6 ^o`

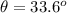
The range of the golf ball is
`R = 190 \ m`

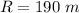
The duration of contact is
`\Delta t = 7.13 \ ms = 7.13 *10^(-3) \ s`

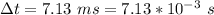
Generally the range of the golf ball is mathematically represented as

`R = (v^2 sin2(\theta))/(g)`

Here v is the velocity with which the golf club propelled it with, making v the subject

`v = \sqrt{(R * g)/(sin 2 (\theta)) }`

=>
`v = \sqrt{(190 * 9.8)/(sin 2 (33.6)) }`

=>
`v = 44.94 \ m/s`

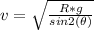
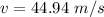
Generally the change in momentum of the golf ball is mathematically represented as

`\Delta p = m * (v - u )`

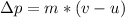
here u is the initial velocity of the ball before being stroked and the value is 0 m/s

`\Delta p = 0.0267 * ( 44.94 - 0 )`

=>
`\Delta p = 1.19996 \ kg \cdot m/s`

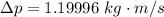
Generally the average force of impact is mathematically represented as

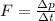
`F = (\Delta p )/(\Delta t)`

=>
`F = (1.19996 )/(7.13 *10^(-3))`

=>
`F = 168.298 \ N`