Question

The weekly amount spent by a small company for in-state travel has approximately a normal distribution with mean $1450 and standard deviation $220. What is the probability that the actual expenses will exceed $1560 in 20 or more weeks during the next year?

Answer 1

0.0903

Explanation:

Given that :

The mean = 1450

The standard deviation = 220

sample mean = 1560

`P(X > 1560) = P( Z > (x - \mu)/(\sigma))`

`P(X > 1560) = P(Z > (1560 - 1450)/(220))`

`P(X > 1560) = P(Z > (110)/(220))`

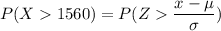
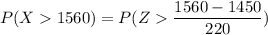
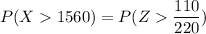
P(X> 1560) = P(Z > 0.5)

P(X> 1560) = 1 - P(Z < 0.5)

From the z tables;

P(X> 1560) = 1 - 0.6915

P(X> 1560) = 0.3085

Let consider the given number of weeks = 52

Mean
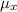`\mu_x` = np = 52 × 0.3085 = 16.042

The standard deviation =
`\sqrt {n \time p (1-p)}`

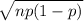
The standard deviation =
`\sqrt {52 * 0.3085 (1-0.3085)}`

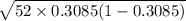
The standard deviation = 3.3306

Let Y be a random variable that proceeds in a binomial distribution, which denotes the number of weeks in a year that exceeds $1560.

Then;

Pr ( Y > 20) = P( z > 20)

`Pr ( Y > 20) = P(Z > (20.5 - 16.042)/(3.3306))`

`Pr ( Y > 20) = P(Z >1 .338)`

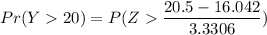
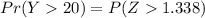
From z tables

P(Y > 20)
`\simeq` 0.0903