Answer:
The length and width of the rectangular garden are 20 feet and 10 feet.
Explanation:
Given that the length of fencing = 60 feet
The area of the garden = 200 sq. feet.
As the length of the fencing is equal to the perimeter of the garden, so the perimeter of the rectangular garden is 60 feet.
Let l and b be the length and width of the rectangular garden.
So, the perimeter of the garden = 2(l+b)=60
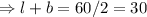
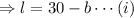
The area of the rectangular garden
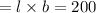
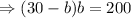 [from equation (i)]
[from equation (i)]
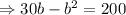
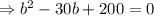
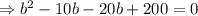
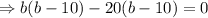
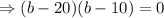

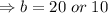
Now, from equation (i),
If b=20 than l= 30-20=10
or if b=10 than l=30-10=20.
Hence, the length and width of the rectangular garden are 20 feet and 10 feet.