Question

A soccer ball is kicked with an initial velocity of 35 m/s at an angle of 60 degrees from the horizontal. How far down the field will the ball hit the ground

Answer 1

The ball will hit the ground 108.25 m down the field

Step-by-step explanation:

To determine how far down the field the ball will hit the ground, that is the Range of the ball. From formula to calculate Range in projectile motion,

`R = (u^(2) sin2\theta )/(g)`

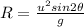
Where R is the Range

u is the initial velocity

θ is the angle of projection

and g is acceleration due to gravity (Take g = 9.8 m/s²)

From the question,

Initial velocity, u = 35 m/s

Angle, θ = 60°

Putting these values into the equation, we get

`R = (35^(2) ( sin2(60)) )/(9.8)`

`R = (1225 * sin(120))/(9.8)`

`R = (1225 * 0.8660)/(9.8)`

`R = (1060.85)/(9.8)`

`R = 108.25 m`

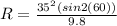
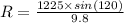
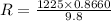
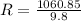
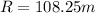
Hence, the ball will hit the ground 108.25 m down the field.