Question

In a hot summer day, a spherical air bubble that has a volume of 1.20 cm3 is released at temperature 17.0 °C by a scuba diver 25.0 m below the surface of ocean. Calculate the radius of the spherical bubble when it reaches the surface at temperature 30 °C? Assume that the number of air molecules in the bubble remain the same (rhosalt water = 1.027 g/cm3 ).

Answer 1

The radius of the bubble when it reaches the surface at 30 ºC is 1.015 centimeters.

Step-by-step explanation:

Let suppose that air bubble behaves as ideal gas, whose equation of state is:

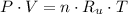`P\cdot V = n\cdot R_(u)\cdot T` (Eq. 1)

Where:

`P` - Pressure of the bubble, measured in kilopascals.

`V` - Volume of the bubble, measured in cubic meters.

`n` - Molar amount of the bubble, measured in kilomoles.

`T` - Temperature, measured in Kelvin.

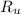`R_(u)` - Ideal gas constant, measured in kilopascal-cubic meter per kilomole-Kelvin.

Then, we eliminate the molar amount and the ideal gas constant by constructing the following relationship:

`(P_(A)\cdot V_(A))/(T_(A)) = (P_(B)\cdot V_(B))/(T_(B))` (Eq. 2)

Where:

`P_(A)`,
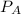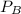`P_(B)` - Pressure of the bubble at bottom and surface, measured in kilopascals.

`V_(A)`,
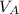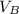`V_(B)` - Volume of the bubble at bottom and surface, measured in cubic meters.

`T_(A)`,
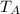`T_(B)` - Temperature of the bubble at bottom and surface, measured in Kelvin.

The pressure experimented by the bubble at bottom and surface are, respectively:

`P_(A) = 101.325\,kPa+\left(1027\,(kg)/(m^(3)) \right)\cdot \left(9.807\,(kg)/(m^(3)) \right)\cdot (25\,m)\cdot \left((1)/(1000)\,(kPa)/(Pa) \right)`

`P_(A) = 353.120\,kPa`

`P_(B) = 101.325\,kPa`

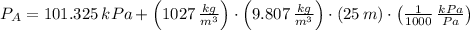
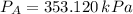
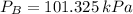
If we know that
`P_(A) = 353.120\,kPa`,
`P_(B) = 101.325\,kPa`,
`V_(A) = 1.20* 10^(-6)\,m^(3)`,
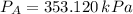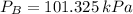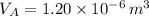`T_(A) = 290.15\,K` and
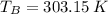`T_(B) = 303.15\,K`, then the volume of the bubble at surface is:

`((353.120\,kPa)\cdot (1.20* 10^(-6)\,m^(3)))/(290.15\,K) = ((101.325\,kPa)\cdot V_(B))/(303.15\,K)`

`1.460* 10^(-6) = 0.334\cdot V_(B)`

`V_(B) = 4.372* 10^(-6)\,m^(3)`

`V_(B) = 4.372\,cm^(3)`

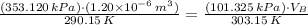
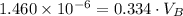
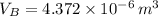
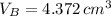
And the volume of the air bubble is determined by this formula:

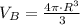`V_(B) = (4\pi\cdot R^(3))/(3)` (Eq. 3)

Where
`R` is the radius of the air bubble, measured in centimeters.

If we know that
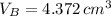`V_(B) = 4.372\,cm^(3)`, then the radius of the air bubble is:

`4.372 = (4\pi\cdot R^(3))/(3)`

`R^(3) = 1.044`

`R \approx 1.015\,cm`

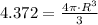
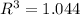
The radius of the bubble when it reaches the surface at 30 ºC is 1.015 centimeters.