Question

A rectangle has a perimeter of 32 in. Find the length and width of the rectangle under which the area is the largest.

a. Let the width to be x and the length to be y , then the quantity to be maximized is (expressed as a function of both x and y) A=_____
b. The condition that x and y must satisfy is y=______

Answer 1

Length of the rectangle is 8 in and the breadth is 8 in.

a.
`A=xy`

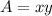
b.
`y=16-x`

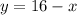
Explanation:

Length = x

Breadth = y

Area is given by
`A=xy`

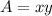
Perimeter of rectangle is given by

`2(x+y)=32\\\Rightarrow x+y=16\\\Rightarrow y=16-x`

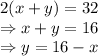
The condition that x and must satisfy is
`y=16-x`

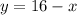
So, area is

`A(x)=x(16-x)\\\Rightarrow A(x)=16x-x^2`

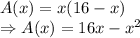
Differentiating with respect to x we get

`A'(x)=16-2x`

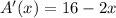
Equating with zero

`0=16-2x\\\Rightarrow x=(16)/(2)\\\Rightarrow x=8`

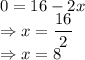
Double derivative of A(x)

`A''(x)=-2`

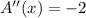
So
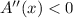`A''(x)<0` which means
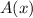`A(x)` is maximum at
`x = 8`

`y=16-x=16-8\\\Rightarrow y=8`

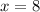
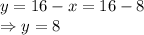
So length of the rectangle is 8 in and the breadth is 8 in.