Question

Find out how long it takes a ​$ investment to double if it is invested at compounded . Round to the nearest tenth of a year. Use the formula . A. years B. years C. years D. years

Answer 1

(A) 8.8 years

Explanation:

Given that the principal amount = $ 3100

Rate of compound interest = 8% compounded semiannually.

The given formula is

`A=P\left(1+(r)/(n)\right)^(nt)`

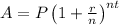
Where A is the final amount, P is the principal amount, r is the rate of compound interest, t is the time and n is the number of times per year the interest is compounded.

From the given condition,

P=$3100

r= 8%=0.08 compounded semiannually

n=2

A=2 x 3100=$ 6200.

Put all these in the given formula to get the required time, we have

`6200=3100\left(1+(0.08)/(2)\right)^(2t)`

`\Rightarrow \left(1+0.04\right)^(2t)=6200/3100`

`\Rightarrow 1.04^(2t)=2\\\\\Rightarrow 2t\log_(10)(1.04)=\log_(10)(2)\\ \\\Rightarrow 2t =(\log_(10)(2))/(\log_(10)(1.04))\\\\\Rightarrow 2t =17.673\\\\\Rightarrow t = 17.673/2=8.8365\\`

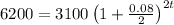
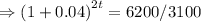
On rounding to the nearest tenth of a year, t=8.8 years.

So, the invested amount will be double in 8.8 years.

Hence, option (A) is correct.