Question

A 306-kg car moving at 16.5 m/s hits from behind a 810-kg car moving at 13.2 m/s in the same direction. If the new speed of the heavier car is 17.5 m/s, what is the velocity of the lighter car after the collision, assuming that any unbalanced forces on the system are negligibly small?

Answer 1

v₂f = 5.1 m/s

Step-by-step explanation:

• Assuming no external forces acting during the collision, total momentum must be conserved.
• ⇒ p₀ = pf
• The initial momentum p₀, can be written as follows:

`p_(o) = m_(1) *v_(1o) + m_(2) *v_(2o) (1)`

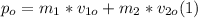
where m₁ = 306 kg, m₂ = 810 kg, v₁₀ = 16.5 m/s, v₂₀ = 13.2 m/s

• The final momentum, pf, can be written as follows:

`p_(f) = m_(1) *v_(1f) + m_(2) *v_(2f) (2)`

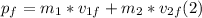
where v₂f = 17.5 m/s

• Since p₀ = pf, which means that (1) is equal to (2),
• Replacing by the givens, and rearranging, we can solve for the only unknown that still remains, v₁f, as follows:

`v_(1f) = v_(1o) +(m_(2) )/(m_(1)) * (v_(2o) - v_(2f) ) \\= 16.5 m/s + (810)/(306) * (13.2 m/s - 17.5 m/s) \\= 16.5 m/s + (810)/(306) * (-4.3 m/s) \\= 16.5 m/s -11.4 m/s = 5.1 m/s`

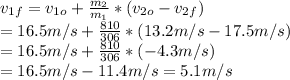
• The velocity of the lighter car after the collision is 5.1 m/s.