Question

On the day a person is born, a deposit of $10,000 is made in a trust fund that pays 5% interest, compound quarterly. Find the balance on the person's 18th birthday.

Answer 1

Given:

Amount deposited on birth = $10,000.

Interest rate = 5% compound quarterly.

To find:

The balance on the person's 18th birthday.

Solution:

The formula for amount is

`A=P\left(1+(r)/(n)\right)^(nt)`

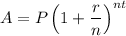
where, P is principal, r is rate of interest, n is number of times interest compounded in an year and t is number of years.

Substitute P=10000, r=0.05, n=4, t=18 in the above formula.

`A=10000\left(1+(0.05)/(4)\right)^(4(18))`

`A=10000\left(1+0.0125\right)^(72)`

`A=10000\left(1.0125\right)^(72)`

`A=24459.2026814`

`A\approx 24459.20`

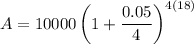
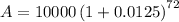
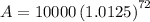
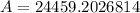
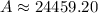
Therefore, the balance on the person's 18th birthday is $24459.20.