Answer:
The required distance away from the foot of the tree is 238.0 feet.
Explanation:
The height of the redwood tree = 340 feet, and the angle of elevation to its top =
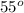 .
.
let the required distance be represented by x, applying the appropriate trigonometry function, we have;
Tan θ =
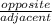
Tan
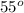 =
=
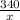
⇒ x =
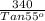
=
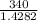
= 238.062
x = 238.0 feet
The required distance away from the foot of the tree is 238.0 feet.