Answer:
A)

B)
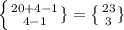
C)
=
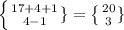
D)
=

Explanation:
A) How many ways can you put all Jellybeans in a row
Total number of Jellybeans = 80
The first jellybeans = 20 yellow , second is 20 orange jellybeans , third is 20 red jellybeans , fourth is 20 green jellybeans
Therefore the number of ways the Jellybeans can be put in a row is :

B) How many ways are there to select a handful of 20 jellybeans
lets assume:
yellow jellybeans = a , orange jellybeans = b , red jellybeans = c , green jellybeans = d
a + b + c + d = 20
This is the number Non-negative integer solutions
=
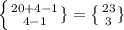
C) This is also the number of Non-negative integer solutions but in this case the value of C ≥ 3
hence the number of ways to select a handful of 20 jellybeans that contains at least 3 red
=
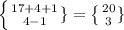
D) In this case the value of C ≥ 3 and B ≤ 2
Hence the number of ways to select a handful of 20 jellybeans that contains at least 3 red and at most 2 orange
=
