Answer:
The value is
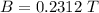
The direction is into the surface
Step-by-step explanation:
From the question we are told that
The mass density is
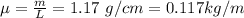
The coefficient of kinetic friction is
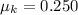
The current the wire carries is
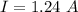
Generally the magnetic force acting on the wire is mathematically represented as
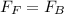
Here
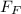 is the frictional force which is mathematically represented as
is the frictional force which is mathematically represented as
While
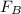 is the magnetic force which is mathematically represented as
is the magnetic force which is mathematically represented as

Here
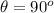 is the angle between the direction of the force and that of the current
is the angle between the direction of the force and that of the current
So
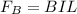
So
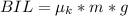
=>
![B = \mu_k * (m)/(L) * [(g)/(I) ]](https://img.qammunity.org/2021/formulas/physics/college/9d14dxy1eplro08qyay9jt8bp8e65qjszl.png)
=>
![B = 0.25 * 0.117 * [(9.8)/(1.24) ]](https://img.qammunity.org/2021/formulas/physics/college/kkhuqwo6jlvel4c1s1h6rr83ohxl3kkajv.png)
=>
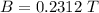
Apply the right hand curling rule , the thumb pointing towards that direction of the current we see that the direction of the magnetic field is into the surface as shown on the first uploaded image