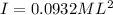Answer:
The value is
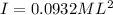
Step-by-step explanation:
From the question we are told that
The rotational inertia about one end is
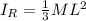
The location of the axis of rotation considered is
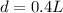
Generally the mass of the portion of the rod from the axis of rotation considered to the end of the rod is

Generally the length of the rod from the its beginning to the axis of rotation consider is
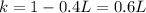
Generally the mass of the portion of the rod from the its beginning to the axis of rotation consider is
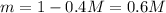
Generally the rotational inertia about the axis of rotation consider for the first portion of the rod is
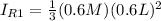

Generally the rotational inertia about the axis of rotation consider for the second portion of the rod is
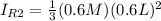
=>
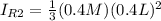
=>
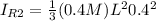
Generally by the principle of superposition that rotational inertia of the rod at the considered axis of rotation is
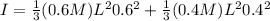
=>
![I = (1)/(3) ML ^2 [0.6 * (0.6)^2 + 0.4 * (0.4)^2 ]](https://img.qammunity.org/2021/formulas/physics/college/vs25z527q1qs4u7xwc08n8gljlop73g3l2.png)
=>