Question

Find the amount to be paid at the end of eight years that is equivalent to a payment of $400 now and a payment of $300 at the end of four years

(a) if 6% simple interest is earned from the date each payment is made and use a comparison date of right now.
(b) if 6% simple interest is earned from the date each payment is made and use a comparison date of eight years from now.
(c) Explain why the fact you get different answers in parts (a) and (b) does not contradict the fact that equations of value at different times are equiv- alent equations.
(d) Repeat parts (a) and (b) except replace "simple interest" with "compound interest."

Answer 1

A) $964

B) $651.35

C) The difference in value for part a and part b is due to time factor and the accumulated interest hence it is better to pay $651.35 right now than to pay $964 when you pay $400 now and $300 in four years time

D) $1016.28 , $637.63

Explanation:

lets assume the amount to be paid in eight years that is equivalent to payment of $400 now and a payment of $300 at the end of four ( 4 ) years ( FV )

a) since a 6% interest is earned each day of every payment

will use this formula : S = P( 1 + rt )

therefore $400 paid today will a simple interest of = 400 * 0.06 * 8 = $192

$300 paid at the end of four years will earn a simple interest of = 300*0.06*4 = $72

hence FV = $ ( 400 + 192 ) + $ ( 300 + 72 ) = $964

b) when compared with eight years from now

PV =
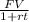`(FV)/(1+rt)` = ($964) / ( 1 + (0.06*8) = $651.35

C) The difference in value for part a and part b is due to time factor and the accumulated interest hence it is better to pay $651.35 right now than to pay $964 when you pay $400 now and $300 in four years time

D) Repeating parts (a) and (b) using compound interest

using the formula : S = P( 1 + r )^t

therefore $400 paid today will have a compound interest of

= 400 ( 1.06)^8 = $637.54

$300 paid at the end of four years will earn a compound interest of

= 300 ( 1.06 ) ^4 = $378.74

hence FV = 637.54 + 378.74 = $1016.28

when compared with eight years from now

=
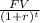`(FV)/((1+r)^t)` = ( 1016.28 ) / ( 1.06 ) ^8 = $637.63