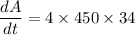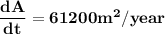Question

An inner city revitalization zone is a rectangle that is twice as long as it is wide. The width of the region is growing at a rate of 34 m per year at a time when the region is 450 m wide. How fast is the area changing at that point in time?

Answer 1

The area is changing at the point of
`\mathbf{61200 m^2/year}`

Explanation:

From the given information:

Let's recall from our previous knowledge that the formula for finding the area of a rectangle = L × w

where;

L = length and w = width of the rectangle

Suppose the Length L is twice the width w

Then L = 2w --- (1)

From The area of a rectangle

A = L × w

A = 2w × w

A = 2w²

Taking the above differentiating with respect to time

`(dA)/(dt )= 4w * (dw)/(dt) --- (2)`

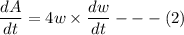
At the time t

`(dw)/(dt)= 34 m \ per \ year ; w = 450 \ m`

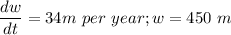
Replacing the values back into equation 2, we get:

`(dA)/(dt )= 4 * 450 * 34`

`\mathbf{(dA)/(dt )= 61200 m^2/year}`