Question

A train slows down as it rounds a sharp horizontal turn, going from 88.0 km/h to 52.0 km/h in the 18.0 s that it takes to round the bend. The radius of the curve is 120 m. Compute the acceleration at the moment the train speed reaches 52.0 km/h. Assume the train continues to slow down at this time at the same rate.

Answer 1

The acceleration at the moment the train speed reaches 52 kilometers per hour is approximately 1.826 meters per square second.

Step-by-step explanation:

According to Rotational Physics, the total acceleration of the train rounding the horizontal turn is a combination of tangential (
`a_(t)`) and radial accelerations (
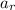`a_(r)`), measured in meters per square second. The former one represents the change in the magnitude of the velocity, whereas the latter one represents the change in its direction. By definition of magnitude and Pythagorean Theorem we get that magnitude of total acceleration (
`a`), measured in meters per square second, is:

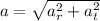`a = \sqrt{a_(r)^(2)+a_(t)^(2)}` (Eq. 1)

Magnitudes of tangential and radial accelerations are determined by using the following formulas:

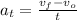`a_(t) = (v_(f)-v_(o))/(t)` (Eq. 1)

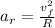`a_(r) = (v_(f)^(2))/(R)` (Eq. 2)

Where:

`v_(o)`,
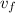`v_(f)` - Initial and final speeds, measured in meters per second.

`t` - Time, measured in seconds.

`R` - Radius, measured in meters.

If we know that
`v_(o) = 24.444\,(m)/(s)`,
`v_(f) = 14.444\,(m)/(s)`,
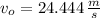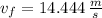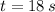`t = 18\,s` and
`R = 120\,m`, then the magnitude of the total acceleration when the train speed reaches 52 kilometers per hour is:

`a_(t) = (14.444\,(m)/(s)-24.444\,(m)/(s) )/(18\,s)`

`a_(t) = -0.556\,(m)/(s^(2))`

`a_(r) = (\left(14.444\,(m)/(s) \right)^(2))/(120\,m)`

`a_(r) = 1.739\,(m)/(s^(2))`

`a = \sqrt{\left(-0.556\,(m)/(s^(2)) \right)^(2)+\left(1.739\,(m)/(s^(2)) \right)^(2)}`

`a \approx 1.826\,(m)/(s^(2))`

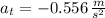
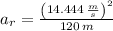
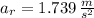
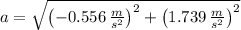
The acceleration at the moment the train speed reaches 52 kilometers per hour is approximately 1.826 meters per square second.