Question

A survey of 80 randomly selected companies asked them to report the annual income of their presidents. Assuming that incomes are normally distributed with a standard deviation of $30,000, determine the 90% confidence interval estimate of the mean annual income of all company presidents. Interpret the statistical results.

Answer 1

The 90% confidence interval estimate of the mean annual income of all company presidents is ($579,545, $590,580).

Explanation:

The information provided is:

`n=80\\\sigma=30,000\\\bar x=585062.50\\\text{Confidence level} = 90\%`

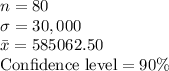
The critical value of z for 90% confidence level is, 1.645.

Compute the 90% confidence interval estimate of the mean annual income of all company presidents as follows:

`CI=\bar x\pm z_(\alpha/2)\cdot(\sigma)/(√(n))\\\\=585062.50\pm 1.645*(30000)/(√(80))\\\\=585062.50\pm5517.50\\\\=(579545, 590580)`

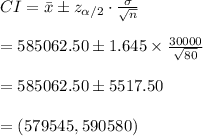
Thus, the 90% confidence interval estimate of the mean annual income of all company presidents is ($579,545, $590,580).

This interval implies that there is 90% probability that the true mean annual income of all company presidents is within this interval.