Question

Mr. Smith's wife works at an animal hospital. There is a equivalent fraction relationship between the number of dogs and cats in the kennels. If there are 20 cats in the kennels, how many dogs?

Answer 1

There are 10 dogs in the kennels

Explanation:

The equivalent fraction relationship between the number of dogs and cats in the kennels is 1/2.

Which means, if
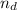`n_d` the number of dods and
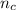`n_c` is the number of cats, then,

`\frac {n_d}{n_c}=(1)/(2)\cdots(i)`

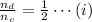
Given that there are 20 cats, so
`n_c=20.`

Now, from equation (i) we have,

`\frac {n_d}{20}=(1)/(2)`

`\Rightarrow n_d=(1)/(2)* 20`

`\Rightarrow n_d= 10`.

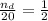
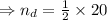
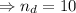Hence, there are 10 dogs in the kennels.