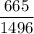Answer:
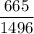
Explanation:
Given : In a group , there are 20 boys and 14 girls.
Total people = 20+14=34
Number of ways to choose 3 people out of 34 =
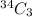
Number of ways to choose 1 girl and 2 boys =
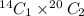
The probability that 1 girl and 2 boys are selected =
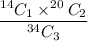
![(14*(20!)/(2!18!))/((34!)/(3!31!))\ \ \ [^nC_r=(n!)/(r!(n-r)!)]\\\\=(14*(20*19)/(2))/((34*33*32*31!)/(3*2\tims3!))\\\\=(665)/(1496)](https://img.qammunity.org/2021/formulas/mathematics/college/ai690epufwd16lqbw95e9bq1zvrkg7wyw1.png)
Hence, required probability =