Question

A flower bed is in the shape of a triangle with one side twice the length of the shortest side and the third side is 19 feet more than the length of the shortest side. Find

the dimensions if the perimeter is 163 feet.
What is the length of the shortest side?
The length of the shortest side is

Answer 1

This is simple as the perimeter is given. All you have to do is make an expression and then equate it to the perimeter.

Side lengths:

Shortest Side:
`x`

1st side:
`2x` (Given that it's twice the length of the shortest of twice of
`x`)

3rd side:
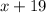`x + 19` (Given that it's 19 more than the length of the shortest side or
`x`)

Since the perimeter is just the addition of all the sides of the shape, the perimeter is going to be the addition of all the expression we made.

So the final expression is going to be:
`x + 2x + x + 19`

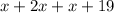
This is nothing but the perimeter so we can therefore equate it to
`163`

`x + 2x + x + 19 = 163`

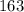
Now we solve the equation. Here it goes!:

`4x + 19 = 163\\4x = 163 - 19\\4x = 144\\x = 144/4 = 36`

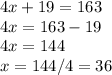
Therefore,
`x = 36`

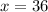
So now we plug them into the previous expressions we made for the sides and you get:

Shortest side:
`36`

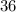
1st side:
`72`

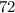
3rd side:
`55`

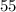
And also, the length of the shortest side is
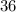`36` as mentioned previously :D