Question

A cylindrical specimen of a brass alloy having a length of 104 mm (4.094 in.) must elongate only 5.20 mm (0.2047 in.) when a tensile load of 101000 N (22710 lbf) is applied. Under these circumstances what must be the radius of the specimen? Consider this brass alloy to have the stress–strain behavior

Answer 1

The radius of the specimen is assumed to be 9.724 mm

Step-by-step explanation:

Given that:

For a cylindrical specimen of a brass alloy;

The length = 104 mm, Elongation = 5.20 mm and the tensile load = 101000 N

Let's first determine the radius of the cylindrical brass alloy from the knowledge of the cross-sectional area of a cylinder.

`A_0 = \pi r ^2`

`r = \sqrt{(A_o)/(\pi)}`

`r = \sqrt{(\bigg ((F)/(\sigma) \bigg ))/(\pi)}`

`r = \sqrt{(F)/( \sigma \pi)}`

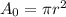
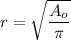
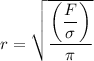
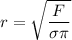
To estimate the tensile stress:

We need to first determine the strain relating to elongation at 5.20 mm

`Strain \ \ \varepsilon= (\Delta l)/(l_o)`

`Strain \ \ \varepsilon= (5.20)/(104)`

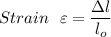
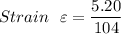
Strain ε = 0.05

Using the stress-strain plot; let assume that under the circumstances;
`\sigma` = 340 MPa for stress corresponding to 0.05 strain

Thus;

The cylindrical brass alloy radius
`r = \sqrt{(F)/( \sigma \pi)}`

`r =\sqrt{ (101000)/((340* 10^(6))\pi)`

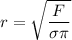
r = 0.009724 m

r = 9.724 mm