Answer:
There is a value of
 in (-1, 1),
in (-1, 1),
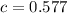 .
.
Explanation:
Let
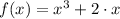 for
for
![x \in[-1,1]](https://img.qammunity.org/2021/formulas/mathematics/college/j94n0ukyvfaxcwhxk5wjse4nv46fjiuwq3.png) , we need to prove that
, we need to prove that
 is continuous and differentiable to apply the Mean Value Theorem. Given that
is continuous and differentiable to apply the Mean Value Theorem. Given that
 is a polynomical function, its domain comprises all real numbers and therefore, function is continuous.
is a polynomical function, its domain comprises all real numbers and therefore, function is continuous.
If
 is differentiable, then
is differentiable, then
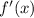 exists for all value of
exists for all value of
 . By definition of derivative, we obtain the following expression:
. By definition of derivative, we obtain the following expression:
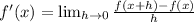
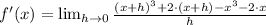

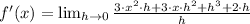
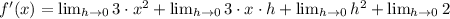
 (Eq. 2)
(Eq. 2)
The derivative of a cubic function is quadratic function, which is also a polynomic function. Hence, the function is differentiable at the given interval.
According to the Mean Value Theorem, the following relationship is fulfilled:
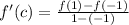 (Eq. 3)
(Eq. 3)
If we know that
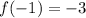 ,
,
 and
and
 , then we expand the definition as follows:
, then we expand the definition as follows:
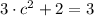
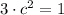
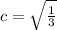

There is a value of
 in the interval (-1, 1),
in the interval (-1, 1),
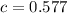 .
.