Question

In the rope climb, a 75 kg athlete climbs a vertical distance of 5.0 m in 9.0 s. What minimum power output was used to accomplish this feat?

___ W

Answer 1

The minimum power output used to accomplish this feat is 408.625 watts.

Explanation:

The minimum power is that needed to overcome potential gravitational energy at constant velocity. From Principle of Energy Conservation, Work-Energy Theorem and definition of power we obtain the following relationship:

`\dot W = m\cdot g \cdot \dot y` (Eq. 1)

Where:

`m` - Mass of the athlete, measured in kilograms.

`g` - Gravitational constant, measured in meters per square second.

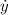`\dot y` - Climbing rate, measured in meters per second.

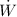`\dot W`- Power, measured in watts.

By the consideration of constant velocity, we get that the climbing rate is represented by:

`\dot y = (s)/(t)` (Eq. 2)

Where:

`s` - Travelled distance, measured in meters.

`t` - Time, measured in seconds.

And by substituting on (Eq. 1), the following expression is found:

`\dot W = (m\cdot g\cdot s)/(t)`

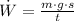
If we know that
`m = 75\,kg`,
`g = 9.807\,(m)/(s^(2))`,
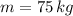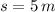`s = 5\,m` and
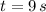`t = 9\,s`, then the minimum power output is:

`\dot W = ((75\,kg)\cdot \left(9.807\,(m)/(s^(2)) \right)\cdot (5\,m))/(9\,s)`

`\dot W = 408.625\,W`

The minimum power output used to accomplish this feat is 408.625 watts.