Question

One atomic mass unit is defined as 1.66 x 10^-27 kg. If a proton has a mass of one atomic mass unit and a density of approximately 5.8 x 10^27 kg/m3^ . What is the diameter of a proton if we assume it is a sphere?

Answer 1

The diameter is
`d = 8.18*10^(-19) \ m`

Step-by-step explanation:

From the question we are told that

The value of one atomic mass unit is
`u = 1.66 *10^(-27) \ kg`

The density of the proton is
`\rho = 5.8 *10^(27) \ kg/m^3`

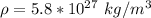
Generally the volume of the proton (sphere)is mathematically represented as

`V = (4)/(3) * \pi * r^3`

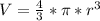
Generally this volume can also be evaluated as

`V = (u)/(\rho)`

=>
`V = (1.66 *10^(-27))/(5.8*10^(27))`

=>
`V = 2.862 *10^(-55) \ m^3`

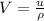
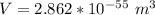
So

`2.862 *10^(-55) = (4)/(3) * 3.142 * r^3`

=>
`r^3 = 6.832 *10^(-56)`

=>
`r = 4.088 *10^(-19) \ m`

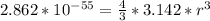
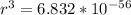
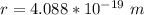
Now the diameter is mathematically represented as

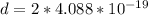
`d = 2 * r`

=>
`d = 2 * 4.088 *10^(-19)`

=>
`d = 8.18*10^(-19) \ m`