Question

The heights of women in the USA are normally distributed with a mean of 64 inches and a standard deviation of 3 inches.

Required:
a. A random sample of six women is selected. What is the probability that the sample mean is greater than 63 inches?
b. What is the probability that a randomly selected woman is taller than 66 inches?
c. What is the probability that the mean height of a random sample of 100 women is greater than 66 inches?

Answer 1

(a) 0.2061

(b) 0.2514

(c) 0

Explanation:

Let X denote the heights of women in the USA.

It is provided that X follows a normal distribution with a mean of 64 inches and a standard deviation of 3 inches.

(a)

Compute the probability that the sample mean is greater than 63 inches as follows:

`P(\bar X>63)=P((\bar X-\mu)/(\sigma/√(n))>(63-64)/(3/√(6)))\\\\=P(Z>-0.82)\\\\=P(Z<0.82)\\\\=0.20611\\\\\approx 0.2061`

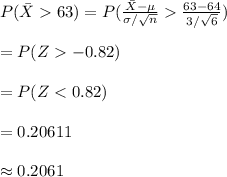
Thus, the probability that the sample mean is greater than 63 inches is 0.2061.

(b)

Compute the probability that a randomly selected woman is taller than 66 inches as follows:

`P(X>66)=P((X-\mu)/(\sigma)>(66-64)/(3))\\\\=P(Z>0.67)\\\\=1-P(Z<0.67)\\\\=1-0.74857\\\\=0.25143\\\\\approx 0.2514`

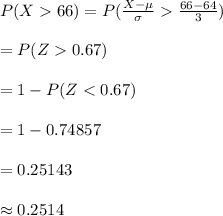
Thus, the probability that a randomly selected woman is taller than 66 inches is 0.2514.

(c)

Compute the probability that the mean height of a random sample of 100 women is greater than 66 inches as follows:

`P(\bar X>66)=P((\bar X-\mu)/(\sigma/√(n))>(66-64)/(3/√(100)))\\\\=P(Z>6.67)\\\\\ =0`

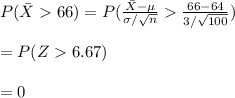
Thus, the probability that the mean height of a random sample of 100 women is greater than 66 inches is 0.