Given:
The sum of three numbers is 12 .
The sum of twice the first number, 3 times the second number, and 4 times the third number is 37 .
The difference between 7 times the first number and the second number is 25.
To find:
The three number.
Solution:
Let the three numbers are x, y and z respectively.
According to the question,
 ...(i)
...(i)
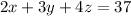 ...(ii)
...(ii)
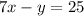 ...(iii)
...(iii)
From (iii), we get
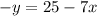
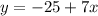
Put
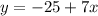 value in (i).
value in (i).


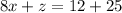
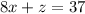 ...(iv)
...(iv)
Put
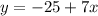 value in (ii).
value in (ii).
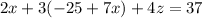
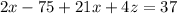
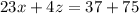
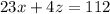 ...(v)
...(v)
Now, Multiply equation (iv) by 4 and subtract the result from (v).
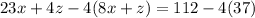


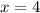
Put x=4 in (iv).
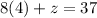
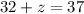
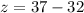
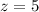
Put x=4 in
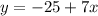 .
.
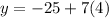

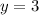
Therefore, the three numbers are 4, 3 and 5 respectively.