Given:
The system of equations is
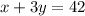 ...(i)
...(i)
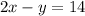 ...(ii)
...(ii)
To find:
The number that must be multiplied with the second equation to eliminate the y-variable.
Solution:
Coefficient of y variable in equation (i) is 3 and in equation (ii) is -1.
To eliminate y-variable the absolute value of coefficients of y-variables should be same.
So, we need to multiply the second equation by 3 to eliminate the y-variable
Multiplying equation (ii) by 3, we get
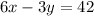 ...(iii)
...(iii)
Adding (i) and (iii), we get
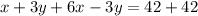
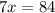
Divide both sides by 7.

Put x=12 in (i).
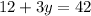
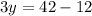
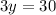
Divide both sides by 10.
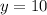
Therefore, x=12 and y=10.