Question

A rancher raises five as many cows as horses. If he has 168 cows and horses, how many cows does he have? Complete the equations below, and then use substitution to solve. Let c represent the number of cows and h represent the number of horses Equation 1: c=_h Equation 2: c+h=_

Answer 1

There are 28 horses and 140 cows

Explanation:

Given

Animals: Cows and Horses

Represent Cows with c and Horses with h

For the first equation, we complete it as thus:

`c = 5h`

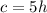
This is so because there are 5 times as many c as h

The second equation will be completed as:

`c + h = 168`

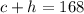
This is so because the total animals are 168

So, we have:

`c = 5h`

`c + h = 168`

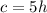
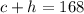
Substitute 5h for c in the second equation

`c + h = 168`

`5h + h = 168`

`6h= 168`

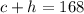
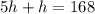
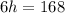
Solve for h

`h = 168/6`

`h = 28`

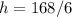
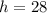
Recall that:

`c = 5h`

`c = 5 * 28`

`c = 140`

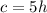
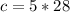
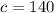
Hence, there are 28 horses and 140 cows