Question

If two balanced die are rolled, the possible outcomes can be represented as follows. (1, 1) (2, 1) (3, 1) (4, 1) (5, 1) (6, 1) (1, 2) (2, 2) (3, 2) (4, 2) (5, 2) (6, 2) (1, 3) (2, 3) (3, 3) (4, 3) (5, 3) (6, 3) (1, 4) (2, 4) (3, 4) (4, 4) (5, 4) (6, 4) (1, 5) (2, 5) (3, 5) (4, 5) (5, 5) (6, 5) (1, 6) (2, 6) (3, 6) (4, 6) (5, 6) (6, 6) Determine the probability that the sum of the dice is 11.

Answer 1

1/18

Explanation:

A die is known to have 6 faces. If n die are rolled, the total number of outcomes or sample space is expressed as;

n(S) =
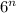`6^n` where;

n is the total number of dies

If two balanced die are rolled, the total number of sample space will be;

n(S) =
`6^2 = 36`

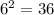
Since we want to to determine the probability that the sum of the dice is 11, the possible outcome or event will be;

n(E) = {(5, 6), (6,5)}

N(E) = 2

Probability = Possible outcome/Total outcome

Probability that the sum of the dice is 11 = n(E)/n(S)

Probability that the sum of the dice is 11 = 2/36

Probability that the sum of the dice is 11 = 1/18